Влияние отклонения центра осыпи от центра цели на поражающую способность выстрела

 

Идеальным случаем поражения цели является покрытие ее центром дробовой осыпи. Для каждого положения цели (движущейся или неподвижной) будет одна единственная точка прицеливания, через которую должна пройти в момент выстрела прицельная линия, чтобы центр осыпи совпал с центром цели. Такого совпадения никогда не бывает на практике, и прицельная линия, благодаря неустранимым ошибкам стрелка, бывает в момент выстрела отклонена от своего идеального положения на больший или меньший угол. Если угол этот не превосходит известной величины, то цель будет перекрыта убойным кругом, в противном случае будет промах или подранение.

Охотнику весьма важно иметь ясное представление о продельных величинах ошибок выцеливания цели. Выцеливать надо только настолько точно, чтобы дичь была бита; излишняя точность ведет лишь к потере времени.

Стремление излишне точно выцеливать дичь препятствует многим стрелять «на вскидку» (т. е., не целясь сознательно), а это уже большой ущерб делу.

Если охотник сумеет определить допустимые предельные ошибки прицеливания и сравнить с ними свои ошибки, получаемые при прицеливании «на вскидку», то он может определенно решить, доступен ли для него с его ружьем этот наиболее совершенный способ стрельбы, а во многих случаях и улучшить но нужной степени прикладистость ружья.

Поражающее действие дробового снаряда отлично от поражающего действия пули. Чтобы убить пулей, надо поразить какой-либо важный для жизни или возможности движения животного орган. Только при крайне больших скоростях имеет, кажется, место явление смертельного действия удара пули, даже и не по жизненно-важным органам (например по кишкам, желудку, легким и т. п.).

Чтобы убить или длительно лишить возможности движения при поражении дробью, нет необходимости поразить жизненно важные органы, достаточно нанести телу дичи достаточное количество достаточно сильных ударов.

Охотничий опыт показывает, что для средней дичи на норм альных охотничьих дистанциях, при соответствующем номере дроби, достаточно 5 попаданий, чтобы надежно взять дичь (Под словом „попадание" здесь и в дальнейшем следует понимать попадание одной дробины. Таким образом "5 попаданий" означает что попало 5 дробин. ). Одно попадание позволяет взять дичь в среднем один раз из десяти.

Из этого следует. что расстояние центра осыпи от центра цели, при ударе снаряда по цели, должно быть небольше такого, при котором в площадь дичи придется около 5 попадании. Этим обусловливается и допустимая ошибка при выце-ливании (сознательном или подсознательном).

Охотник, не боящийся затратить известный труд, может, при помощи изложенного ниже способа, определить достаточно точно допустимые отклонения, учитывая действительный бой своего ружья. Составленные мною номограммы (графики для вычислений) делают этот способ доступным каждому охотнику.

Способ состоит в следующем: на рис. 7 изображена утка пораженная осыпью, центр которой находится в расстоянии r₀ —см. от центра ее тушки (или в r₀ / L * 100% от дистанции L). Утка будет, следовательно, поражена дробинами кольца осыпи, радиусы которого будут: внешний на половину длины тушки больше величины отклонения r₀ , а внутренний—на половину длины тушки меньше. Если обозначим длину тушки через l см, то

r₂ =r₀ + l / 2 и r₁ = r₀ - l / 2

Если мы сумеем найти, сколько дробин попадает в кольцо r₂— r₁то найдем и сколько дробин попадет в тушку дичи, так как в нее попадет дробин во столько раз меньше, чем в кольцо, во сколько раз площадь ее меньше площади кольца.

Найти, сколько дробин попадает в кольцо, можно, если знать радиус круга, включающего лучшую половину (50%) попаданий осыпи, т. е. попаданий, наименее отклоненных от центра осыпи. Радиус этот принято обозначать R₅₀ . Как определить его практически, будет сказано ниже.

Изучение характера распределения попаданий в дробовой осыпи показывает, что, несмотря на кажущуюся случайность и беспорядочность, они распределяются по ней весьма точно, повинуясь определенному закону. Закон этот дает зависимость между процентом попаданий в круг произвольного радиуса и отношением этого радиуса к радиусу круга, включающего лучшую половину попаданий—R₅₀ .

Это значит, что для каждого K = r / R₅₀—существует определенный процент попаданий—р%, как бы ни изменялась величина R₅₀, дистанция стрельбы, номер дроби и т. п.

До K = r / R₅₀ (=) 1,2 закон этот практически один и для осыпи цилиндра и для осыпи чоков. Дальше начинается расхождение, зависящее от величины сгущения осыпи к центру.

В конце кн. на рис.8 изображена теоретическая кривая распределения отклонений, имеющих место при осыпи из строгого цилиндра ружья большого калибра. На вертикальной оси отложены отношения K = r / R₅₀, а на горизонтальной—проценты попаданий в круги радиусов r. Если, например, r вдвое больше R₅₀ , т. е. K = r / R₅₀ = 2 , то в круг радиуса r попадает 94% дробин заряда. Если вдвое меньше—18% и т. п.

Кривая эта представляет из себя общую кривую распределения отклонений любых случайных событий (кривая Гаусса).

Чтобы убедить охотников в глубоком практическом значении этой чисто теоретической кривой, я нанес на нее проценты попаданий, вычисленные по действительным осыпям (140 выстрелов). Из таблички, помещенной в правом верхнем углу диаграммы, видно, что осыпи получены были двумя номерами дроби (№ 7 и № 3), на дистанциях от 20 до 50 м, т. е. при самых разнообразных условиях, и тем не менее точки, соответствующие процентам попаданий, поразительно совпадают с теоретической кривой, отходя от нее, более или менее значительно и опять таки вполне закономерно, лишь на близких дистанциях.

Диаграмма рис. 8 является прекрасным доказательством практической полезности, столь презираемой многими охотниками «теории». Закон, выведенный ученым математиком Гауссом, возможно никогда не державшим в руках ружья, выведенный на основании отвлеченных соображений о распределении случайных событий, оказался полностью применим к дробовой осыпи и позволяет охотнику, вместо утомительного нахождения всей кривой распределения попаданий, ограничиваться нахождением толь ко R₅₀ .

Кривая рис. 8 вполне определяет осыпь цилиндра, для чока же необходимо ввести поправку в часть кривой для K = r / R₅₀ больше 1,2. Дело в том, что дробины осыпи чока находятся не в одинаковых условиях: крайние дробины получают от скоса чока толчок по направлению к оси полета, поэтому закон распределения, выведенный в предположении одинаковости условий, в которых находятся все учитываемые события (в данном случае—дробины заряда), в его чистом виде здесь не применим. На рис. 8 пунктиром тире-точка-тире нанесена кривая распределения попаданий для нормального чока V= 3 — 3,5 (см. ниже гл. 9). Строго говоря, кривая, эта должна быть нанесена и для K = r / R₅₀ —меньшего 1,2, но практически отступления в этой части ничтожны.

Итак, практически величина R₅₀и две кривые рис. 8 вполне определяют характер осыпи и, пользуясь ими, легко найти, сколько попаданий придется в кольцо r₂ — r₁ , перекрывающее дичь при ударе по ней дробового снаряда.

Для определения количества попаданий в тушку дичи при различных отклонениях центра осыпи от центра цели (r₀ ) служат номограммы № 1, 2 и 3, рис. 9, 10 и 11 (см. в конце книги).

При помощи номограммы № 1 находится процент попаданий в кольцо r₂ — r₁ (т. е. р₀ %).

Для нахождения р₀ % надо найти

r₂ = r₁ + l / 2

и

r₁ = r₀ - l / 2

вычислить

К₂ = r₂ /R₅₀

и

К₁ =r₁ /R₅₀ ,

найти по кривой соответствующие полученным К ₂ и К ₁ - p₂ % , и р₁ % и, вычтя p₁ % из p₂ %, определить р₀ %.

 

 

В таблице № 1 приведены площади длины и поперечники дичи. Звездочкой отмечены непосредственные измерения, произведенные мною. И площадь и длина в моих измерениях относятся только к самой тушке, без перьев, а также без шеи и головы (рис. 12). В площади, заимствованной из Журне и Гражд. Инженера, включены вероятно и шеи и головы.

Таблица №1.

Дичь	Площадь S см2	Длина l см	Поперечник (высота) h см
Перепел *	23	8	4
Бекас	40 (Журне)	-	-
Вальдшнеп *	65- 70	12,5	6
Рябчик*	65- 70	13—14	6,5
Сер. куроп. *	75- 80	12,5-13	7-7,5
Бел. куроп. *	90—100	14—15	8-8,5
Тетерев *	140—150	21	9-10
Фазан	230 (Журне)	-	-
Заяц	410—460 (Гр. Инж. и Журне)	-	-
Дрофа	530 (Гр.Инж.)	-	-
Лисица	700 (Журне)	-	-
Кряковой селезень *	134—145	21-22	9
Шилохвость*	115-125	21	8—8,5
Свиязь *	115-125	20	8
Нырок красноголовый *	80	16,5	6,5
Чирок трескунок *	50	13	5

 

При помощи этой таблицы можно определить r₂ = r₁ + l / 2 и r₁ = r₀ - l / 2 ( l длина тушки дичи). Следует, впрочем, иметь в виду, что не будет очень большой погрешности, если просто брать ширину кольца равной 10 см. для мелкой дичи (до куропатки) и 20 см. для более крупной.

Найдя r₂и r₁, следует по левой половине номограммы № 1 найти K ₂ = r₂ /R₅₀ и К₁ = r₁ /R₅₀. Для этого достаточно провести линию, соединяющую деление, соответствующее величине r₂или r₁на левой вертикальной скале АВ с делением, соответствующим R₅₀ , взятым на наклонной скале АС, и продолжить эту линию до пересечения с правой вертикальной скалой СО.

Линия пересечет скалу СО на делении, соответствующем k = r / R₅₀

На номограмме пунктиром тире-точка-тире дан пример вычисления К₂ и К₁ для r₀ = 40 см, 1=16 см и R₅₀ =20 см K₂==2,4 и K₁ ==1,6.

Правая сторона номограммы предназначена для нахождения процентов попаданий в круги радиуса r по найденному К=r / R₅₀

Сплошной линией вычерчена уже известная нам из рис. 8 кривая, по которой, следовательно, надо определять p% для осыпей цилиндра и слабых чоков, а пунктиром нанесена кривая для чоков. Кривая для чоков является, к сожалению, приблизительной, так как мне не удалось к сроку получить нужных данных для нанесения кривых, соответствующих различным степеням сгущения к центру. Однако для практических целей при сгущении V от 3 до 3,5 (см. ниже гл. 9) достаточно и нанесенных кривых. На дистанциях 45—50 м осыпь чока сравнивается по характеру распределения попаданий с осыпью цилиндра, и в этих случаях для чока надо пользоваться сплошной кривой.

Начиная приблизительно с p = 90 %, кривые очень круто загибаются вниз, и пользование ими вследствие этого делается неудобным. Поэтому нижние части кривых повторены еще раз в масштабе для р% в 10 раз большем. Благодаря этому кривые вытянулись, и отсчет по ним можно уже делать достаточно точно. Деления для втянутых кривых нанесены снизу горизонтальной скалы EF.

Чтобы найти р% соответствующие какому либо К= r / R₅₀ надо от деления, К полученного на скале CD, провести горизонтальную линию до пересечения с соответствующей кривой, а из точки пересечения провести вертикальную линию до пересечения с горизонтальными скалами. На номограмме № 1 дан пример вычисления р%, при чем ход решения указан стрелками. Найдя по номограмме № 1 р₂ и р₁ % и вычтя их одно из другого, получим процент попаданий в кольцо радиусов r₂— r₁ :

p%=(p₂ - p₁)%

После этого надо по номограмме № 2 (рис. 10) найти площадь дичи, выраженную в процентах (q%) от площади кольца r₂r₁

Вычисление это производится по формуле:

q%=S*100 / 2* п * r₀ * l

где S см ² — площадь тушки дичи l — -длина тушки и r₀ — отклонение центра осыпи от центра цели. п - число Пи

При пользовании номограммой № 2, все вычисления сводятся к проведению 2-х линий аb —от деления на левой вертикальной скале АВ, соотвествующего r₀ , через деление на-наклонной скале АС, соответствующего l или вообще ( r₂ — r₁, если вместо l берется какая - либо другая величина, например 10 или 20 см, как было сказано выше), до пересечения со средней вертикальной линией CD. Из точки пересечения аb с CD проводится линия bc , соединяющая точку b с делением на правой вертикальной скале EF соответствующим площади тушки дичи — S. Тогда линия bc отметит на наклонной скале СЕ деление, соответствующее искомому проценту—q%- И на этой номограмме дан пример, показывающий ход решения.

Теперь нам известны P% и q% и надо перейти к номограмме №3 (рис. 11), по которой находится искомое количество попаданий в тушку дичи.

Левая половина номограммы № 3 служит для нахождения количества попаданий в кольцо r₂ — r₁ , по количеству дробин в заряде N шт. и найденному проценту попаданий в кольцо р%, а правая для нахождения количества попаданий п_д в тушку дичи, по количеству попаданий в кольцо п_p и проценту q%. Соответствующая формула будет:

n_д = N.p.q. / 100.00

При пользовании номограммой №3 дело сводится опять только к проведению 2 линий ab и bс.

Линия ab соединяет деление на скале АВ, соответствующее количеству дробин в заряде с делением на наклонной скале АС, соответствующим р₀% (найденным по номограмме № 1)продолжается до пересечения со средней вертикальной линией CD в точке b. Линия bc соединяет найденную точку b с делением на наклонной скале СЕ, соответствующим q% (найденным по номограмме № 2) и идет до пересечения со скалой ЕF, на которой и указывает деление, соответствующее количеству попаданий в тушку дичи— n_д .

При пользовании номограммой нет необходимости проводить линии: достаточно только поворачивать линейку (лучше прозрачную) около острия карандаша, поставленного в соответствующую точку. Так, при решении примера, данного на номограмме № 3, поступаем следующим образом: ставим карандаш в точку d на деление скалы АС, соответствующее p₀=20%, и прикладываем к нему линейку так, чтобы она прошла и через деление скалы АВ, соответствующее N =360 шт. Затем, удерживая линейку на месте, переносим острие карандаша в точку b , на линии CD, и поворачиваем вокруг него линейку так, чтобы она прошла через деление скалы CE соответствующее q = 5%. Линейка укажет на скале EF искомое деление п_д= 3,6 дробины.

Необходимо иметь в виду еще следующее: иногда может случиться, что на скале не будет нужного деления (например, на скале АВ номограммы № 3 нет делений для количества дробин в заряде N= 400 шт.). Тогда можно взять деление вдвое меньше и вдвое увеличить результат. Можно поступить и иначе: взять на какой-либо другой скале деление вдвое большее— тогда результат получится сразу верный. На номограмме № 3 линией тире-три-точки-тире дано построение для решения того же примера при N, взятом вдвое меньше (180 вместо 360).

К этому приему — брать на скале не нужное деление, а больше или меньше, следует прибегать и в тех случаях, когда линия построения располагается почему - либо неудобно: очень косо пересекает скалы, проходит через слишком мелкие деления наклонных скал и т. п. Только величины K=r / R₅₀ на номограмме № 1 надо брать обязательно те самые, которые получатся от деления r на R₅₀ .

Пользуясь изложенным способом, охотник может основательно проанализировать осыпь своего ружья на разных дистанциях и определить пределы поражающей способности своего ружья и своего искусства. При этом нет необходимости определять R₅₀ для разных дистанций, достаточно определить для обычной дистанции L — 35 м, a R₅₀ для других дистанций найти, пользуясь номограммой № 4 (рис. 13). На левой части этой номограммы нанесены кривые, дающие отношения R'₅₀ на разных дистанциях к R₅₀ на дистанции L — 35 м. Проведя вертикальную линию от деления нижней горизонтальной скалы АС, соответствующего той дистанции— L м, для которой требуется найти R₅₀ , находим точку пересечения ее с кривой и из этой точки проводим линию вправо, до пересечения со средней вертикальной скалой CD, на которой она отметит деление, соответствующее отношению R₅₀ на дистанции L м к R₅₀ на дистанции 35 м. В приведенном на номограмме примере отношение это равна s=l,5 (L = 45 м, чок).

Правая половина номограммы № 4 служит для вычисления искомого R'₅₀ по известному R₅₀ на 35 м. Соответствующая формула будет:

R'₅₀ = s * R₅₀

При пользовании номограммой № 4 достаточно соединить линией деление на вертикальной средней скале CD, coответствующее найденному s = R'₅₀ / R₅₀, с делением на наклонной скале СЕ, соответствующим величине известного R₅₀см на дистанции 35 м. Продолжив эту линию до пересечения с правой вертикальной скалой EF, мы найдем на ней деление, соответствующее искомому R'₅₀ см на дистанции L м.

Результаты отдельных выстрелов могут довольно значительно разниться от результатов, вычисленных теоретически, но в среднем точность будет вполне достаточна для практических целей.

Определить R₅₀ для осыпи своего ружья можно различными способами. Самым простым будет следующий: стрельба производится по достаточно большим листам бумаги, вмещающим не менее 80—90% дробин заряда. Находится центр осыпи, для чего проводятся вертикальная и горизонтальная линии, отделяющие слева и справа, сверху и снизу по 50°/о попаданий.

 

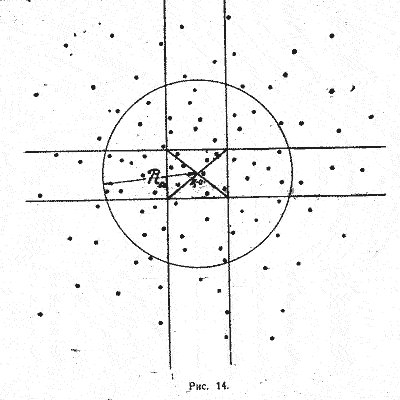
Точка их пересечений и будет центром осыпи. Чтоб не считать предварительно всех попаданий в листе, можно отсчитывать слева и справа, сверху и снизу по какому - либо количеству дробин, немного меньшему 50% заряда, тогда линии, отделяющие эти количества, образуют в пересечении прямоугольник (рис.14). Пресекая этот прямоугольник с угла на угол двумя линиями (диагоналями), получим, с достаточной для практика точностью, центр осыпи в точке пересечения диагоналей.

Из центра осыпи надо провести окружность: если стрельба ведется на дистанции в 35 м, то радиусом около 25—29 см для чока и около 40—45 см для цилиндра.

В этих кругах окажется около 50% дробин заряда и нетрудно будет соответственно увеличить или уменьшить круг, чтобы найти вмещающий 50% дробин заряда (а не 50°/о попаданий в мишень!), радиус которого и будет искомым R₅₀, .

Если под руками будет настоящая книга, то подбирать круг не придется. Определив % дробин, попавших во взятый произвольно круг, можно по кривым рис. 8 найти К=r / R₅₀ а отсюда вычислить и R₅₀ по номограмме № 1. R₅₀ надо определять по результатам не менее как 5 выстрелов.

Для изучения характера осыпи было бы много удобнее вести пристрелку не на общепринятой дистанции 35 м, а на более близкой—метров 20—25. На этих дистанциях на листе умещается вся осыпь, характер ее очень ясно виден, ясно виден и снос, если он имеется. Пересчитать потом количество попаданий на любую дистанцию, как мы уже теперь знаем, не представляет никакого труда: по номограмме № 4 (рис. 13) находим по R₅₀ , определенному, например, на L=20 mm R₅₀ 35 м, а по этому R₅₀ можем расчертить и всю осыпь на этой дистанции. Пусть, например, на дистанции в 20 м R₅₀, чока оказался равным 14 см. Сколько придется попаданий в пойманную мишень диаметром 75 см, на дистанции 35 м? По левой половине номограммы № 4 (рис. 13) находим s = R₅₀ ' / R₅₀ = 0,46 .

Соединяем линией деление s=0,46 на скале СD с делением 14 на скале EF линия эта пересечет наклонную скалу СЕ на делении 30,5. Следовательно R₅₀ на дистанции 35 м будeт равен 30.5 см

Диаметр нормальной мишени равен 75 см., а радиус r= 37.5 см. Находим:

K= r / R₅₀ = 37.5 / 30.5 = 1.23

По кривой номограммы № 4 (рис. 13) находим, что К = 1.23 соответствует процент попаданий Р — 64—65%

Если N=350 шт то внормальную мишень попадает около225 шт

Анализ количества попаданий в тушку при резличных ошибках прицеливания позволяет сделать весьма интерес-ные и практически полезные выводы. На рис. 15,16 и 17 даны кривые количества попаданий в вальдшнепа и рябчика дробью № 9 и № 7 и в тетерева и крякового селезня дробью № 5. На вертикальной оси отложены количества попаданий, а на горизонталь-нои-дистанции. Кривые вычерчены для чока и цилиндра и для ошибок прицеливания в 0,5%,1%, 1,5% от дистанции Вероятная ошибка около 1 % L соответствует очень хорошему стрелку, берущему до 75% стреленой дичи; стрелок, имеющий вероятную ошибкуоколо 1,5% , берет не более 50%

Ошибку 0,5% L и меньше очень хорошие стрелки делают в 16% выстрелов, а средние только в 7% Что же показывают эти кривые?

Во-первых: для стрелка с вероятной ошибкой в 1,5% цилиндр навсех дистанциях имеет преимущество перед чоком. Для него, стало быть, чок уместен только для более или менее прицельных выстрелов по неподвижной дичи, и, в крайнем случае, для второго выстрела. На вскидку из чока стрелять ему совсем не следует. Для очень хорошего стрелка чок и цилиндр приблизительно равноценны, но так как в 50% выстрелов он делает ошибку меньше 1%, а преимущество чока растет по мере уменьшения ошибки, то для него чок все таки уместен и позволит ему бить дичь более чисто на дистанциях свыше 25 м Во-вторых, что особенно интересно, по мере Увеличения дистанции уменьшается преимущество, даваемое стрелку его искусством, и на предельной охотничьей дистанции в 50 м результаты у всех стрелков получаются приблизительно одинаковые и, что особенно важно, недостаточные для надежного взятия дичи (только 0.5 — 3 дробины). Это заставляет сделать заключение, что стрелять «на вскидку» каждому стрелку следует только на определенной дистанции. Дистанция эта для очень хорошего стрелка будет не более 35 м, а для среднего — 25 - 30 м. Стрельба «на вскидку» на более далеких дистанциях сопровождается недопустимо большим количеством подранков.

 

 

В-третьих: средний стрелок (с вероятной ошибкой в 1,5%) вообще бьет дичь недостаточно надежно. Из этого можно сделать для него полезный вывод: не следует :валивать вину на ружье и рассказывать сказки про «ж и в я-щ и е» ружья, а лучше путем упражнения и улучшения прикла-дистости ружья стремиться уменьшить свою вероятную ошибку. Тогда и ружье перестанет «живить».

 

 

Освоившись с изложенным в настоящей главе и в следующей ниже главе о значении прикладистости, охотник сможет определить, каков должен быть характер осыпи его ружья при различных условиях охоты.

Осыпь должна быть такова, чтобы при возможно большой ошибке прицеливания дичь все-таки была бита достаточно надежно.

 

 

Как мы теперь знаем, для большинства охотников это будет осыпь цилиндра и, во всяком случае, не та осыпь с 75—80% кучности, о которой мечтает и которой неразумно добивается это большинство.

Этот естественный вывод часто встречает возражение, что он «неспортивен». С точки зрения охоты-спорта интересно преодоление известных трудностей и удачный выстрел из кучно-бьющего ружья, да еще 20 кал, да еще на сверхдальней дистанции, много «спортивнее» легкого выстрела из цилиндра 12 кал па 25—30 м. Говорящие так забывают, что об'ектом их спортивных упражнений в данном случае являются не футболь-ные мячи, а живые существа, которых они десятками калечат, чтобы взять единицы. Охота таких спортсменов действительно является злой и нехорошей забавой.