3.3. Дробовая осыпь

Если произвести единичный выстрел дробью по достаточно большой мишени на некотором от нее расстоянии, то можно обнаружить, что пробоины расположены крайне хаотично. Такой же выстрел по другой мишени мало изменит наши представления об осыпи. Однако несколько (3-5 и более) выстрелов по одной и той же мишени позволят увидеть совсем другую картину. Прежде всего, видно, что дробь концентрируется в центре мишени и с увеличением расстояния от центра к периферии плотность дроби - количество дробин приходящих на единицу площади мишени - убывает. Далее, прослеживается центральная симметрия, то есть ни одно направление от центра к краям осыпи не является предпочтительным. Если из центра осыпи описывать окружности того или иного радиуса, то они будут охватывать тем больше дробин, чем больше радиус окружности. Поэтому, всегда найдется такой радиус круга, который будет охватывать, например, половину числа дробин в снаряде или даже все 100%.

Так как при стрельбе дробью число дробин в снаряде достигает многих десятков, а то и сотен штук, то результаты стрельбы, несмотря на уникальность каждого отдельного выстрела, вполне закономерны и подчиняются распределению Релея (закон Гаусса на плоскости).

Плотность распределения случайной величины в двумерном пространстве, имеющей центральную симметрию, может быть, согласно закону Релея, представлена в виде

f(R)= AR2^-(R/R₅₀⁾², 3.1

где R - расстояние от центра осыпи дроби до какой-либо точки осыпи;

R₅₀ - радиус круга, охватывающий 50% числа дробинок в снаряде, а

А - нормирующий множитель, обеспечивающий равенство

АR2^-(R/R₅₀⁾²dR = 1. 3.2

Интегрирование 3.2, дает

А =ln2/R₅₀², 3.3

где ln2 - натуральный логарифм числа 2, равный 0,6931...,

Тогда 3.1, с учетом 3.3, будет иметь окончательный вид

f(R)= ln2/R₅₀² . R2^-(R/R₅₀⁾² 3.4

По поводу формул 3.1-3.4 необходимо сказать следующее. Как известно, в законе Релея основанием показательной функции принято не число 2, как в формуле 3.1, а основание натуральных логарифмов е=2,718... Однако формула 3.1, тем не менее, описывает тот же самый нормальный закон, но с другим коэффициентом А и другим коэффициентом в показателе степени. И еще. Нормальный закон распределения относится к непрерывным функциям, мы же будем иметь дело с дискретными величинами, поэтому в дальнейшем под дискретной величиной будем понимать ее математическое ожидание, округляя полученные значения в ту или иную сторону до целой величины. Так, например, число 17,36 дробины следует считать 17-ю дробинами, а 17,63 дробины - 18-ю. Выбор цифры 2 вместо е оказывается, с одной стороны, более удобным для вычислений, а с другой - и это самое главное, - радиус R₅₀, охватывающий центральную часть дроби в осыпи, оказывается настолько репрезентативным, что через R₅₀ можно выражать многие параметры не только дробовой осыпи, но и дробового выстрела в целом.

Зная плотность распределения дроби в осыпи, число дробин в снаряде и размер площади цели можно путем интегрирования 3.4 по контуру цели на каком-либо расстоянии от центра (теоретически в любом месте пространства) найти вероятность попадания числа дробин в эту площадь. В общем случае такое интегрирование затруднено, однако в частных случаях, когда цель имеет вид круга с центром, совпадающим с центром осыпи, или кольца с радиусами R₁ и R₂ или части этого кольца_, то результат интегрирования может быть выражен в элементарных функциях.

Найдем вероятность попадания числа дробин N в круг радиуса R. Если число дробин в снаряде N_0, то, согласно 3.4,

N = N₀ln2/R₅₀² .2^-(R/R₅₀⁾²RdR = N₀(1-2^-(R/R₅₀⁾²) 3.5

В некоторых случаях возникает необходимость найти число дробин в кольце с внутренним радиусом R₁ и наружным радиусом R₂. Тогда, согласно 3.5,это можно сделать по следующей формуле

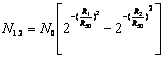. 3.6

Из формулы 3.5 может быть найдено математическое ожидание плотности дроби на расстоянии R от центра осыпи.

Плотность дроби Σ_к на расстоянии R от центра равна отношению числа дробин dN к площади dS кольца с радиусом R и шириной dR

Σ_к = dN/dS. 3.7

Поскольку dN, как следует из формулы 3.5, равен

dN = 2RN₀ln2/R₅₀²2^(R/R₅₀⁾²dR,

а dS (из формулы площади круга R²) равен 2RdR то, подставляя dN и dS в 3.7, получим

_к = N₀ln2/R₅₀².2^(R/R₅₀⁾². 3.8

Практически можно обходиться вообще без интегрирования. Для этого достаточно умножить величину интересующей площади цели S_д на плотность вероятности 3.4.

N = N₀ln2S_д/R₅₀².2^(R/R₅₀⁾².

Если эквивалентный радиус цели R_э, равный S_д/, не превосходит R₅₀/3, то погрешность вычисления при этом не превосходит 3-3,5%. В дальнейшем будет показано, что для практики допустима погрешность и до ±5%.

Величина R₅₀ зависит, прежде всего, от расстояния до цели, от типа сверловки ствола и способа снаряжения патронов. Величина R₅₀ непосредственно связана с кучностью, хотя и не является таковой. Чем больше кучность, тем меньше величина R₅₀ и наоборот.

Обозначим N/N₀ = у, а R/R₅₀ = х, тогда выражение 3.5 будет иметь вид

y = 1 - 2^-x² 3.9

Это аналитическое выражение на рисунке 6 представлено в виде сплошной линии. Значками на этом рисунке обозначены результаты, полученные разными авторами независимо друг от друга, из ружей разных калибров на разных расстояниях разными номерами дроби и их числом в снаряде.

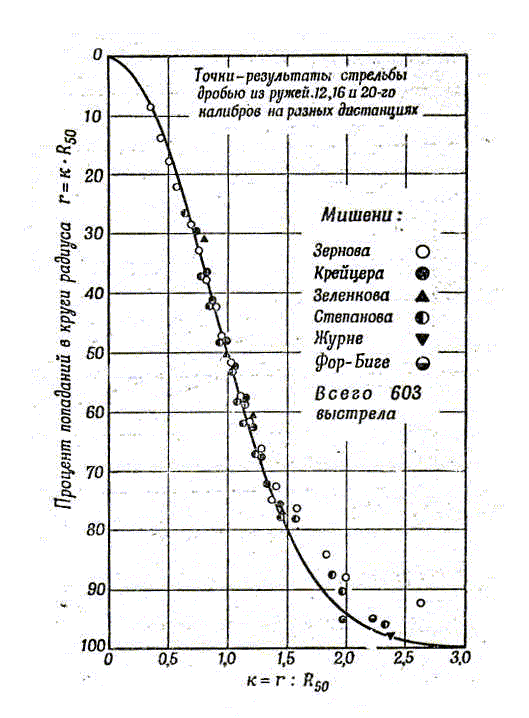Рисунок 6. Экспериментальные данные, полученные   разными авторами независимо друг от друга из разных ружей разными снарядами. Аналитическое выражение показано сплошной линией.

Как видно из рисунка, аналитическое выражение хорошо согласуется с экспериментальными данными вплоть до R = 1,5R₅₀, который охватывает 80% дробин снаряда. Остальная часть дроби, находящаяся за пределами, так называемого, убойного круга (в дальнейшем этому понятию будет дано четкое определение) не представляет большого значения.

Зависимость параметра R₅₀ от расстояния L до цели так же хорошо изучена и для каждой сверловки ствола может быть представлена в виде следующих эмпирических формул

- для цилиндра R₅₀ = 0,60L^1.23

- для цилиндра с напором R₅₀ = 0,50L^1,26

- для 0,25 чока R₅₀ = 0,40L^1,29

- для 0,5 чока R₅₀ = 0,25L^1,39

- для 0,75 чока R₅₀ = 0,20L^1,41

- для полного чока R₅₀ = 0,13L^1,50

На рис.7 эти зависимости в том же порядке сверху вниз представлены в виде семейства кривых для расстояний от 10 до 60 метров. Было замечено так же некоторое увеличение рассеивания мелкой дроби, нежели крупной. М.Журнэ эту зависимость выразил в следующем виде: «Произведение величины рассеивания дроби на корень квадратный ее диаметра есть величина постоянная». Аналитически это выглядит так

R₅₀= C,

где C - константа,

d - диаметр дроби.

Поскольку диаметр дроби №9 равен 2 мм, а диаметр дроби №0000 равен 5 мм, то величина R₅₀ при этом изменяется относительно дроби №4 (диаметр 3,25 мм) всего на 30%, что в некоторых случаях можно не учитывать.