1.4. Сопротивление движению снаряда в стволе

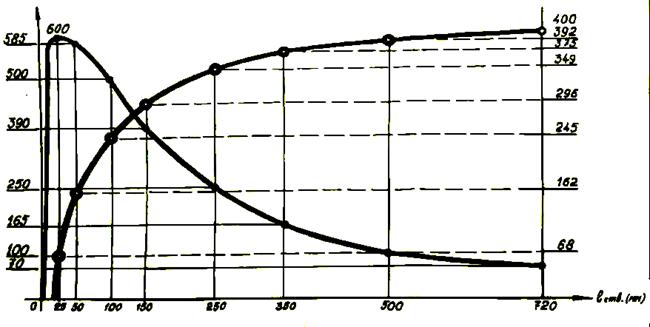
На рисунке 1, взятом из упомянутой книги «Ижевские ружья», изображены зависимости давления пороховых газов, и скорости движения снаряда дроби от расстояния до казенной части ствола. Из рисунка видно, что на участке от 50 см до 72 см скорость изменилась на 8 м/с, а средняя скорость на этом участке была 396 м/с. Следовательно, снаряд этот участок пролетел за 5,6.10^-4 с. Отсюда ускорение равно не 145 м/с², как указано авторами, а 14400 м/с². Но даже для создания такого ускорения достаточно всего 19 бар. Но среднее давление на этом участке было 85 бар. Следовательно, на этом участке на снаряд действовало противодавление равное 66 бар.

Это противодавление, по моему мнению, возникает за счет давления воздуха перед снарядом при его движении по каналу ствола. Положение усугубляется еще и тем, что перед снарядом находятся пороховые газы, прорвавшиеся между пыжом и каналом ствола. Сопротивление движению снаряда этой составляющей общего сопротивления можно считать пропорциональной квадрату скорости снаряда. На это, в частности, указывал Э.В.Штейнгольд в книге «Все об охотничьем ружье»: «При выстреле снаряд выталкивает из канала ствола находящийся там воздух и сжимает его...». Вся внешняя баллистика артиллерийских снарядов и пуль только тем и занимается, что исследует влияние на снаряд ускорения силы тяжести и сил сопротивления воздуха в открытом пространстве. Понятно, что в полузамкнутом объеме это влияние должно увеличиться многократно. В этой связи хочу напомнить общеизвестные факты раздутия стволов от попадания в них таких, казалось бы, безобидных предметов как легкий пыж или рыхлый снег. В одном случае я был свидетелем, когда приятель засунул в ствол тростинку и выстрелил, чтобы посмотреть, как далеко она полетит. Дело кончилось раздутием ствола перед чоком. В другом случае, в котором я сам был участником, от клочка ваты, вставленного в дуло, ствол в средней части просто разорвало.

Другой составляющей силы сопротивления движению снаряда, безусловно, является сухое трение (в отличие от вязкого трения, которого в стволе не усматривается). Его величина равна коэффициенту трения, умноженного на силу нормального давления. Коэффициенты трения свинца по стали и полиэтилена по стали примерно одинаковы и равны 0,25-0,3, однако силу нормального давления дроби при выстреле измерить не удается. На трение в нарезном стволе расходуется от 15 до 25% энергии пороха, трение же в гладком стволе вследствие расклинивания дроби может превышать эти величины в 1,5-2 раза, достигая 40%. В следующем разделе «Давление форсирования» сила трения оценивается в 1600 Н, что на длине ствола 0,72 м составляет порядка 1100 Дж. Пак как общие потери составляют 2300 Дж, то на аэродинамическое сопротивление приходится до 1200 Дж.

В статье «Отдача при выстреле - хорошо знакомая, но мало понятная?», опубликованной в интернете www.sportguns.ru/10-02/otdacha/html, А.Володаренко пишет: «В стволах, различающихся только длиной при одинаковых порохах, график давления в начале будет абсолютно идентичен (ведь не может же дробь заранее «знать» - долго ли ей еще лететь по стволу или нет)». К сожалению, автор не одинок. Имеется даже порочная методика определения давлений и скоростей путем укорачивания ствола (статья «Внутренняя баллистика» К.Мартино в «Российской охотничьей газете», №46, 14-20.11.2001г). Смею заверить, что снаряд «знает», не в пример нам, и очень хорошо, что его тормозит, о чем мы можем только догадываться и строить гипотезы.

Итак, положим аэродинамическое сопротивление движению снаряда пропорциональным квадрату скорости. Такое сопротивление наблюдается при достаточно больших скоростях движения, в отличие от ламинарного сопротивления, пропорционального первой степени скорости.

Запишем уравнение 1.16 в виде

В = dV/dt + СV², 1.29

где В = рs/М - ускорение, м/с²,

СV² - торможение, м/с².

Тогда получим

VdV/dx = В - СV². 1.30

Интегрирование дает

ln(B/(B-СV²)= 2Сx. 1.31

Решая 1.31 относительно V, найдем

V² = B/С(е^2Сх/М- 1)/ е^2Сх/М 1.32

Из 1.32 следует, что при t=0 V=0, а при t V²B/C = V_мах².

Ранее было получено V_мах = 758 м/с, х_к+l = 0,149 м и V_к = 378 м/с. Подставляя эти значения в формулу 1.32, можно найти величину С, которая равна 0,959. Подставляя величину С и длину ствола L в выражение 1.32, найдем дульную скорость с учетом сопротивления движению снаряда, которая оказалась равной 475 м/с. С учетом сухого трения начальная скорость должна уменьшиться до 410 м/с. Таким образом, результат оказался довольно близким к исходному значению.

Хочу, однако, заметить, что эти результаты все же носят приближенный характер. С одной стороны, это связано с рядом сделанных допущений, без которых аналитическое решение задачи было бы невозможным. С другой стороны, приходится пользоваться средними значениями входящих в формулы величин, которые для конкретного пороха могут отличаться в ту или иную сторону. Мои попытки связаться с патронными заводами для получения натурных данных по внутренней баллистике пока не увенчались успехом. К имеющимся литературным источникам я отношусь осторожно, поскольку они носят описательный характер и часто не соответствуют друг другу. Все же меня не покидает надежда вернуться к этому вопросу после получения более точных экспериментальных данных.